Approximating kernel-weighted proportions in PostGIS
Imagine you want compare various locations in terms of the availability of a certain type of environment, such as fresh water.
You might want to use a measure of the proximity of that environment — such as the nearest neighbour distance.
You might want to use a measure of the quantity of that environment in the vicinity — such as the proportion of land within a specific radius that is of that type.
Or you might ideally like a measure that combines both of these: one that incorporates the quantity of that environment, but gives greater weight to areas that are nearer, and lesser weight to those that are further away.
In that third case, what you probably want is a kernel-weighted proportion.
How it works
In this usage, a ‘kernel’ just means a distribution function, such as the normal (Gaussian), triangular, or Epanechnikov. The kernel is used to decide what weight should be attached to places at varying distances from the location under consideration.
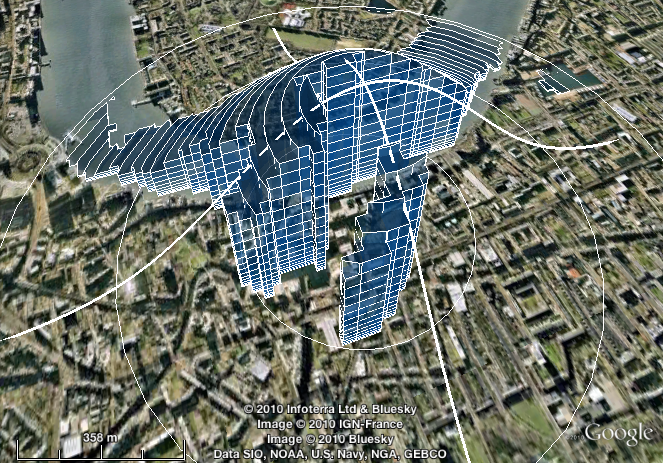
I find it helpful to imagine the weight assigned to each point as a third dimension: the height at each point. I then imagine the kernel as a solid object positioned with its centre over the point I’m measuring from. For the normal or Epanechnikov kernels, this object is bell-shaped; for the triangular kernel, it’s a cone; for the (trivial) uniform kernel, it’s a cylinder.
The total volume of this object is the denominator of the kernel-weighted proportion. Now I imagine removing all parts of the object that don’t lie directly above the type of environment being measured. The volume of the remaining parts of the object — those directly overlying the environment of interest — is the numerator of the kernel-weighted proportion.
Implementation in PostGIS
The following SQL functions enable you to approximate kernel-weighted proportions in PostGIS. They do so by splitting the 3-dimensional kernel into horizontal slices of equal height, but with radii differing according to the kernel and kernel parameters specified. They calculate the summed volume of the intersections of the slices with the supplied polygons, and divide that by the total summed volume of the complete slices. (Assign each slice a height of 1 and these volumes are helpfully the same as the areas).
This approach is illustrated, for the normal kernel, at the top of this post.
-- kernel functions create or replace function uniform_pdf ( double precision -- $1 = x , double precision default 1.0 -- $2 = bandwidth , double precision default 0.0 -- $3 = centre ) returns double precision as $$ select case when $1 > $3 - $2 and $1 < $3 + $2 then ( select cast(0.5 as double precision) ) else 0 end; $$ language sql immutable; create or replace function triangular_pdf ( double precision -- $1 = x , double precision default 1.0 -- $2 = bandwidth , double precision default 0.0 -- $3 = centre ) returns double precision as $$ select case when $1 > $3 - $2 and $1 < $3 + $2 then ( select 1 - abs(($1 - $3) / $2) ) else 0 end; $$ language sql immutable; create or replace function normal_pdf ( double precision -- $1 = x , double precision default 1.0 -- $2 = std dev (bandwidth) , double precision default 0.0 -- $3 = mean (centre) ) returns double precision as $$ select (1.0 / (sqrt(2.0 * pi() * pow($2, 2)))) * exp(-pow($1 - $3, 2) / (2.0 * pow($2, 2))); $$ language sql immutable; create or replace function epanechnikov_pdf ( double precision -- $1 = x , double precision default 1.0 -- $2 = bandwidth , double precision default 0.0 -- $3 = centre ) returns double precision as $$ select case when $1 > $3 - $2 and $1 < $3 + $2 then ( select 0.75 * (1 - pow(($1 - $3) / $2, 2)) ) else 0 end; $$ language sql immutable; -- current kernel function -- (uncomment the kernel you want to use, and redefine: the normal is shown here) create or replace function __current_kernel_pdf ( double precision -- $1 = x , double precision default 1.0 -- $2 = std dev/bandwidth , double precision default 0.0 -- $3 = mean/centre ) returns double precision as $$ select normal_pdf -- epanechnikov_pdf -- triangular_pdf -- uniform_pdf ($1, $2, $3); $$ language sql immutable; -- support functions create or replace function __slice_height ( double precision -- $1 = kernel std dev , double precision -- $2 = kernel radius at top of slice , double precision -- $3 = kernel radius at bottom of slice ) returns double precision as $$ select __current_kernel_pdf($2, $1) - __current_kernel_pdf($3, $1); $$ language sql immutable; create or replace function __slice_radius ( double precision -- $1 = kernel radius at top of slice , double precision -- $2 = kernel radius at bottom of slice ) returns double precision as $$ select $1 + (($2 - $1) / 2); $$ language sql immutable; create or replace function __kernel_slice_volume ( double precision -- $1 = kernel std dev , double precision -- $2 = kernel radius at top of slice , double precision -- $3 = kernel radius at bottom of slice , int -- $4 = buffer precision ) returns double precision as $$ select coalesce( st_area( st_buffer( st_makepoint(0, 0), __slice_radius($2, $3), $4 ) ), 0 ) * __slice_height($1, $2, $3); $$ language sql immutable; create or replace function __intersected_slice_volume ( geometry -- $1 = area geometry , geometry -- $2 = kernel centre point geometry , double precision -- $3 = kernel std dev , double precision -- $4 = kernel radius at top of slice , double precision -- $5 = kernel radius at bottom of slice , int -- $6 = buffer precision ) returns double precision as $$ select coalesce( st_area( st_intersection( $1, st_buffer( $2, __slice_radius($4, $5), $6 ) ) ), 0 ) * __slice_height($3, $4, $5); $$ language sql immutable; -- main function create or replace function kernel_weighted_local_proportion ( geometry -- $1 = area geometry , geometry -- $2 = kernel centre point geometry , double precision -- $3 = kernel std dev , double precision -- $4 = truncation bandwidth (for normal only -- for others, repeat $3) , int -- $5 = number of horizontal slices for approximation (for uniform, use 1) , int -- $6 = buffer precision (number of points per 1/4 circle) ) returns double precision as $$ select sum(__intersected_slice_volume( $1, $2, $3, $4 * (cast(s as double precision) / $5), -- kernel radius at top of slice $4 * (cast(s + 1 as double precision) / $5), -- kernel radius at bottom of slice $6 )) / sum(__kernel_slice_volume( $3, $4 * (cast(s as double precision) / $5), -- kernel radius at top of slice $4 * (cast(s + 1 as double precision) / $5), -- kernel radius at bottom of slice $6 )) from generate_series(0, $5 - 1) s; $$ language sql immutable; |